The Statistics of Active Matter: The Panic Model and Active Glass Mixtures

 In its original form, Gibbs-Boltzmann statistical mechanics cannot describe “active matter,” such as living, driven, or self-propelled systems. Contemporary models of swarming and flocking behaviors, where self-propelled objects like rods spontaneously form patterns, are conceptually simple but practically complicated.  While these models can imitate pattern formation they do a poor job explaining how or why it occurs.

To what extent do flocking transitions have an

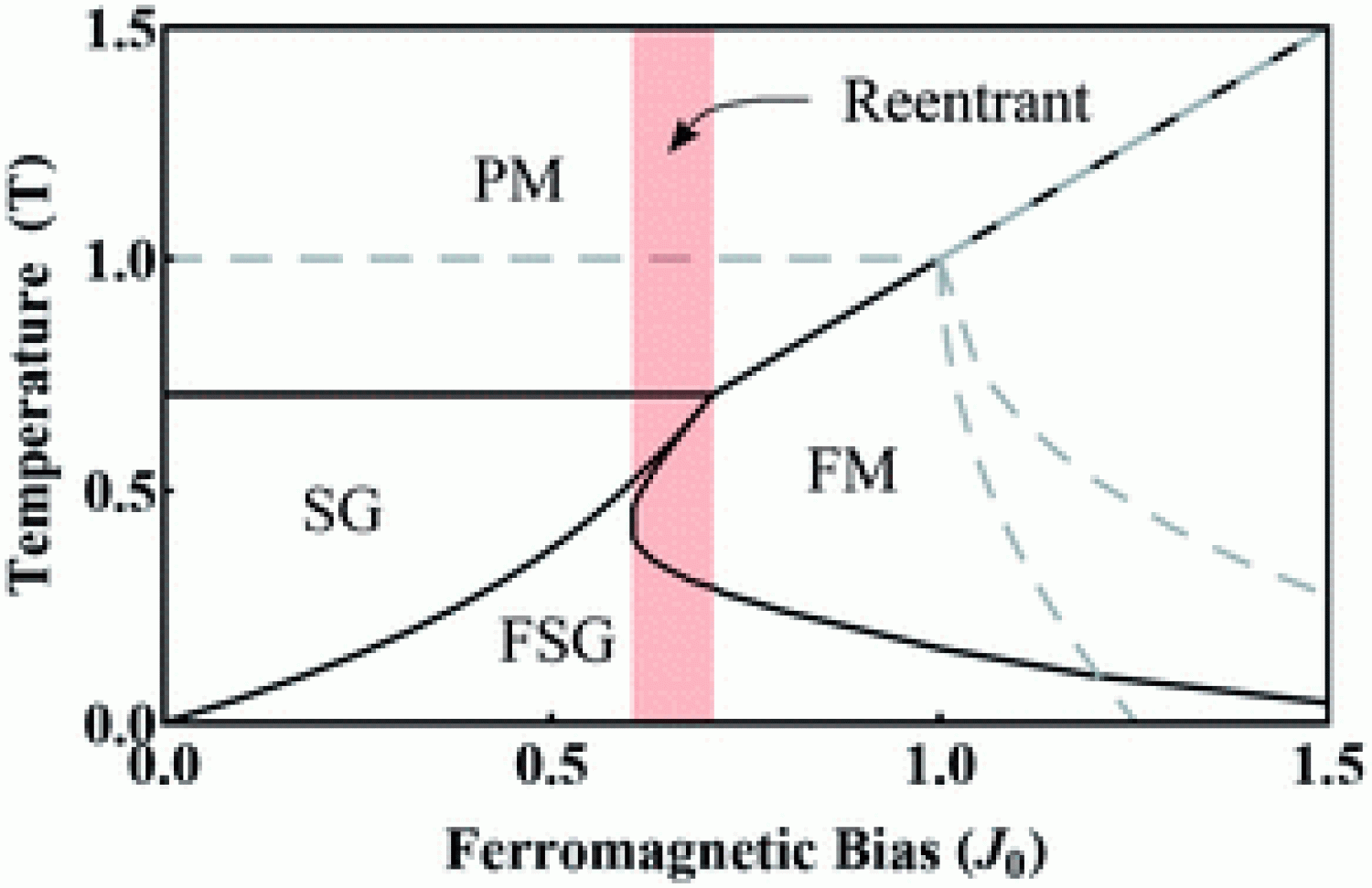
figure
figure
underlying thermodynamic origin and to what extent is the transition to a flocked state a purely dynamical phenomenon?  To help answer this question, my group devised a simple two-dimensional lattice model, which we called the “panic model,” that displays robust spontaneous ordering even though it is a thermodynamic ideal gas.[1]  Our work shows that flocking transitions can be purely dynamical in nature even though the phenomenology of the pattern formation mechanisms, like nucleation and growth, bear striking resemblance to those encountered in thermodynamic phase transitions.  In the panic model the irreversible spontaneous flocking transitions derive from the violation of detailed balance for active systems. 

Glasses and active systems form the bookends of dynamically arrested states in nonequilibrium systems, but both exhibit myriad stable states that are kinetically estranged from one another. We thought it would be interesting to study a mixture of the two systems, so we generalized the canonical Sherrington-Kirkpatrick spin glass model and analyzed it by modifying the replica trick.[2] Perhaps most interestingly, there is a region in the phase diagram where the interactions between the inactive and active phase can overpower the frustrated interactions of the glassy inactive state.  When this happens, the glass melts under cooling. We are currently looking to see if this phenomenon, called reentrance, occurs in molecular analogs by designing molecular dynamics simulations for mixtures of active and glassy colloids.  Our work shows that the interactions between frustrated and active phases may provide subtle, unusual, and previously unanticipated ways for systems to alter their mechanical properties by amplifying small fluctuations in the active phase.  The results of our efforts in this area may well have applications to materials science and to cellular and tissue bioengineering.

  1. Piliewicz, K. R. and Eaves, J. D., Flocking with Minimal Cooperativity: The Panic Model. Physical Review E, 2014. 89(1): p.012718
  2. Piliewicz, K. R. and Eaves, J. D., Reentrance in an Active Glass Mixture. Soft Matter, 2014. 10(38): p. 7495-7501.